Rammelen aan de wijsbegeerte
Houdt Hempel ons voor de gek?
• • • • • • • • •
[K.T. Dröfe: Rammelen aan de wijsbegeerte p. 25]
Als Everitt en Fisher in hun boek Modern Epistemology de problemen van de inductie aan de orde stellen, maken zij melding van de paradox van Hempel.1 Deze epistemoloog beoogt met het formuleren van de naar hem genoemde paradox inductie als methode van kennisverwerving aan de kaak te stellen. De consequenties van de paradox zijn inderdaad zo vreemdsoortig dat men geneigd is te veronderstellen dat er werkelijk iets mis is met deze methode. Zo volgt uit de paradox volgens Hempel dat een witte zakdoek een bijdrage levert aan de waarschijnlijkheid van het zwart zijn van raven. Dat is op het eerste gezicht natuurlijk te gek voor woorden. Hier wordt niettemin betoogd dat het waar is, maar wel op een geheel andere manier dan Hempel ons wil doen geloven.
De strekking van dit artikel is (voor een moment uitgaande van de vooronderstelling dat de gevolgde redenering klopt), dat niet door Hempel is aangetoond dat inductie als methode kwalijke bijverschijnselen vertoont. Laten we om te beginnen de paradox eens aanschouwen. In de weergave van Everitt en Fisher ziet deze er, in een vrije vertaling, zo uit:
(a) Alle A’s zijn B.
(b) Alle niet-B’s zijn niet-A.
(1) (a) En (b) zijn logisch equivalent. (premisse)
(2) Iedere X die Y is, bevestigt (tot op zekere hoogte)
de bewering dat alle X-en Y’s zijn. (premisse: Het gaat hier
om het principe van inductie berustend op het vergaren
van waarnemingen en dat begint met de eerste.)
Dus (3) Iedere niet-B die niet-A is, bevestigt (tot op zekere hoogte)
de bewering dat alle niet-B’s niet-A’s zijn. [uit (2)]
(4) Dat wat de bewering p bevestigt, bevestigt in dezelfde mate
iedere aan p equivalente bewering. (premisse)
Dus (5) Iedere niet-B die een niet-A is bevestigt (tot op zekere hoogte)
dat alle A’s B zijn. [uit (1), (3) en (4)]
Dus (6) Ieder niet-zwart ding dat een niet-raaf is, bevestigt (tot op
zekere hoogte) dat alle niet-zwarte dingen niet-raven zijn.
[uit (5)]2
Dus (7) Ieder niet-zwart ding dat een niet-raaf is, bevestigt (tot op
zekere hoogte) dat alle raven zwart zijn. [uit (1), (4) en (6)]
Dus (8) Een witte zakdoek (i.c. een niet zwart ding dat een niet-raaf is)
bevestigt (tot op zekere hoogte) dat alle raven zwart zijn.
[uit (7)]
We zien dus, zo vervolgen Everitt en Fisher, dat onschuldig ogende premissen (1), (2) en (4) leiden tot bizarre conclusies op een manier die strikt logisch lijkt. Zij geven toe dat de conclusie vreemd is, maar houden het er toch op dat de gevolgde gedachtegang binnen de grenzen van de logica ligt. De bewering onder (1) roept misschien enig ongeloof op. Is het echt waar dat (a) en (b) logisch equivalent zijn? De auteurs menen van wel en lichten dit punt als volgt toe met behulp van deze Venn-diagrammen:
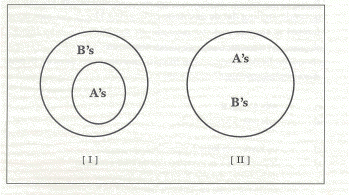
Als alle A’s B’s zijn dan geldt het volgende:
of (a) Er zijn enige B’s die niet A zijn (weergegeven in [i])
of (b) Er zijn geen B’s die geen A zijn (weergegeven in [ii])
Hoe de zaken ook liggen, alles dat buiten de B-cirkel valt, valt ook buiten de A-cirkel. Dus als alle A’s B’s zijn, dan zijn alle niet-B’s niet-A’s. Ook (4) verdient enige toelichting: Het gaat erom dat equivalentie impliceert dat als van (a) en (b) één waar is de ander ook waar moet zijn en als van (a) en (b) één niet waar is ook de ander niet waar kan zijn.
Poging tot bestrijding van Hempels betoog
Wat Hempel in feite doet is in regel (6) een nieuw gegeven invoeren. Hij introduceert hier raven en vermeldt, zij het indirect, dat zij zwart zijn. Daarnaast, zegt hij, zijn er velerlei niet zwarte dingen, en dat zijn allemaal niet-raven. Welke conclusie kun je nu trekken als je een witte zakdoek vindt? Antwoord: Dat er raven zijn en dat zij zwart zijn. Is dit een inductieve conclusie? Nee, het is zuivere deductie. De ene witte zakdoek bevestigt met 100% zekerheid dat er zwarte raven zijn. Het volgt gewoon uit het in (6) binnengesmokkelde gegeven. Duidelijker wordt het misschien nog als we een eindig aantal werelden aannemen en de mogelijke verschijnselen beperken tot de twee zaken die in de paradox voorkomen: zwarte raven en witte zakdoeken. Er zijn werelden waar deze twee verschijnselen aanwezig zijn en er zijn lege werelden, nemen we aan. We bezoeken een aantal werelden en komen op zeker moment in een wereld waar we een witte zakdoek aantreffen. Er kan nu deductief en dus met volstrekte zekerheid geconcludeerd worden dat er ook raven voorkomen in deze wereld en bovendien dat zij zwart zijn.
Laten we eens een ander verschijnsel bij de kop nemen en de formulering van de paradox strak volgen. Wij komen de paradox binnen bij regel 6:
(6) Alle dingen die geen wielen bezitten en geen auto zijn, bevestigen
(tot op zekere hoogte) dat alles wat geen wielen heeft geen auto is.
(Merk op dat hier impliciet gesteld wordt dat auto’s wielen hebben.)
(7) Alle dingen die geen wielen hebben en geen auto zijn, bevestigen
(tot op zekere hoogte) dat auto’s wielen hebben.
(8) Een wandelstok (i.e. een ding zonder wielen) bevestigt
(tot op zekere hoogte) dat alle auto’s wielen hebben.
Gesteld kan worden dat de redenering klopt met uitzondering van de beperkende bepaling ‘tot op zekere hoogte’. Deze kan gevoeglijk achterwege worden gelaten. Eerst hebben we de verschijnselen beperkt tot auto’s en wandelstokken. Nu introduceren we een groot aantal andere verschijnselen. In die wereld komen we een telefoon tegen en weer weten we meteen dat auto’s wielen hebben. Vervolgens komen we even helemaal niets tegen. En toch weten we al dat auto’s wielen hebben. Hoe komt het dat we dat weten? Omdat het impliciet gegeven is. De gedachtegang heeft, zo lijkt het, weinig met inductie uit te staan.
Laten we voor de zekerheid ook nog eens naar knikkers kijken. Die kunnen letterlijk alle kleuren hebben inclusief zwart maar niet wit (nemen we even aan). Op basis van de formule kunnen we nu stellen: Alle knikkers hebben kleur. In de paradox bij (6) vullen we in: Alles wat geen kleur heeft (en dus wit is) is geen knikker. We komen weer een witte zakdoek tegen. Wat zegt deze over de kleur van knikkers. Niets. Over de kleur van knikkers valt niets te concluderen en wel omdat over de kleur van knikkers niets gegeven wordt. (Als de kleur van raven niet gegeven zou zijn, en zij dus ook wit zouden kunnen zijn, konden witte zakdoeken ten aanzien van de kleur van raven met de beste wil van de wereld niets indiceren.) En als we het nu eens zo proberen: Alle zwarte knikkers zijn zwart. Alles wat niet zwart is, is geen zwarte knikker. Wat vertelt ons nu de groene knikker over zwarte knikkers? Inderdaad, het is tijd om te stoppen. We komen steeds tot dezelfde conclusie: De witte zakdoek, de wandelstok en de groene knikker vertellen niets wat we niet al wisten en er kan geen sprake zijn van inductie.
Er zijn eigenlijk maar twee reële mogelijkheden: Of de hier geboden gedachtegang faalt (en daar wordt ernstig rekening mee gehouden), of Hempel houdt ons gewoon voor de gek, want als de uiteenzetting niet faalt heeft hij natuurlijk zelf al lang doorzien dat zijn paradox niet klopt en stelt hij er gewoon genoegen in ons om de tuin te leiden. En verder kunnen we, zo lijkt het, op grond van de volgende redenering nog iets over Hempel concluderen: Iedereen die geen hekel heeft aan de inductieve methode ontwerpt geen tegen inductie gerichte paradox. Iemand die wel een tegen inductie gerichte paradox ontwerpt, bevestigt (tot op zekere hoogte) dat hij een hekel heeft aan de inductieve methode.
mei 1996
Noten
1. Everitt en Fisher: Modern Epistemology p.159 e.v.
2. Waarschijnlijk is hier een vergissing in het spel, want (6) volgt niet zo zeer uit (5) maar veeleer uit (3).